Bela

Was ist Bela?

Bela ist ein super “Spielzeug” wenn man an digitaler Signalverarbeitung oder Soundprocessing interessiert ist. Trockene Theorie wird direkt hörbar und damit sehr viel einfacher verständlich.

Auf einem Beaglebone läuft hierzu ein Linux mit einer Echzeiterweiterung. Zusätzlich steckt ein Tochterboard auf dem Beaglebone der die AD - bzw DA-Wandlung in hoher Auflösung durchführt. Damit kann man das Board z.B. zwischen eine Audioquelle und eine Endstufe einschleifen bzw. einen Kopfhörer anschließen.

Ähnlich wie beim Arduino gibt es Funktionen für die Initialisierung, die zyklische Abarbeitung und den Shutdown. In diese Funktionen ergänzt man seinen eigenen Code. Und ebenso wie beim Arduino gibt es eine Menge fertiger Klassen und Bibliotheken.

Das Board wird per USB an den eigenen Rechner angeschlossen. Die integrierte Entwicklungsumgebung ist dann per Webbrowser direkt vom Board verfügbar. D.h. man braucht auf dem PC nichts zu installieren.

Tutorial

Besonders empfehlenswert ist es die Tutorial Serie https://learn.bela.io/tutorials/ durchzuarbeiten. Hier bekommt man in didaktisch sehr gut aufbereiteten Videos eine umfassende Einführung und alles Wissenswerte, um mit Bela zu arbeiten.

Beispiel

Was sich mathematisch so liest: $y = a_{1} * sin(\frac{2 * \pi * f_{1}}{f_{samp}}) + a_{2} * sin(\frac{2 * \pi * (2*f_{1})}{f_{samp}})$

Wird im folgenden Code-Ausschnitt umgesetzt. Es werden zwei Sinusfrequenzen erzeugt. Diese werden aufaddiert und dann auf die Stereoausgänge und das Software-Scope ausgegeben.

   	// This for() loop goes through all the samples in the block
	for (unsigned int n = 0; n < context->audioFrames; n++) {
	    // Increment the phase by one sample's worth at this frequency
		gPhase1 += 2.0 * M_PI * frequency / context->audioSampleRate;
		gPhase2 += 2.0 * M_PI * 2*frequency / context->audioSampleRate;
		
		if(gPhase1 >= 2.0 * M_PI)
			gPhase1 -= 2.0 * M_PI;
			
		if(gPhase2 >= 2.0 * M_PI)
			gPhase2 -= 2.0 * M_PI;			

		// Calculate a sample of the sine wave
		float out = amplitude * sin(gPhase1) +  amplitude* sin(gPhase2);

		// Store the sample in the audio output buffer
	    audioWrite(context, n, 0, out);
	    audioWrite(context, n, 1, out);
	    
	    // Write the output to the oscilloscope
    	gScope.log(out);
    }

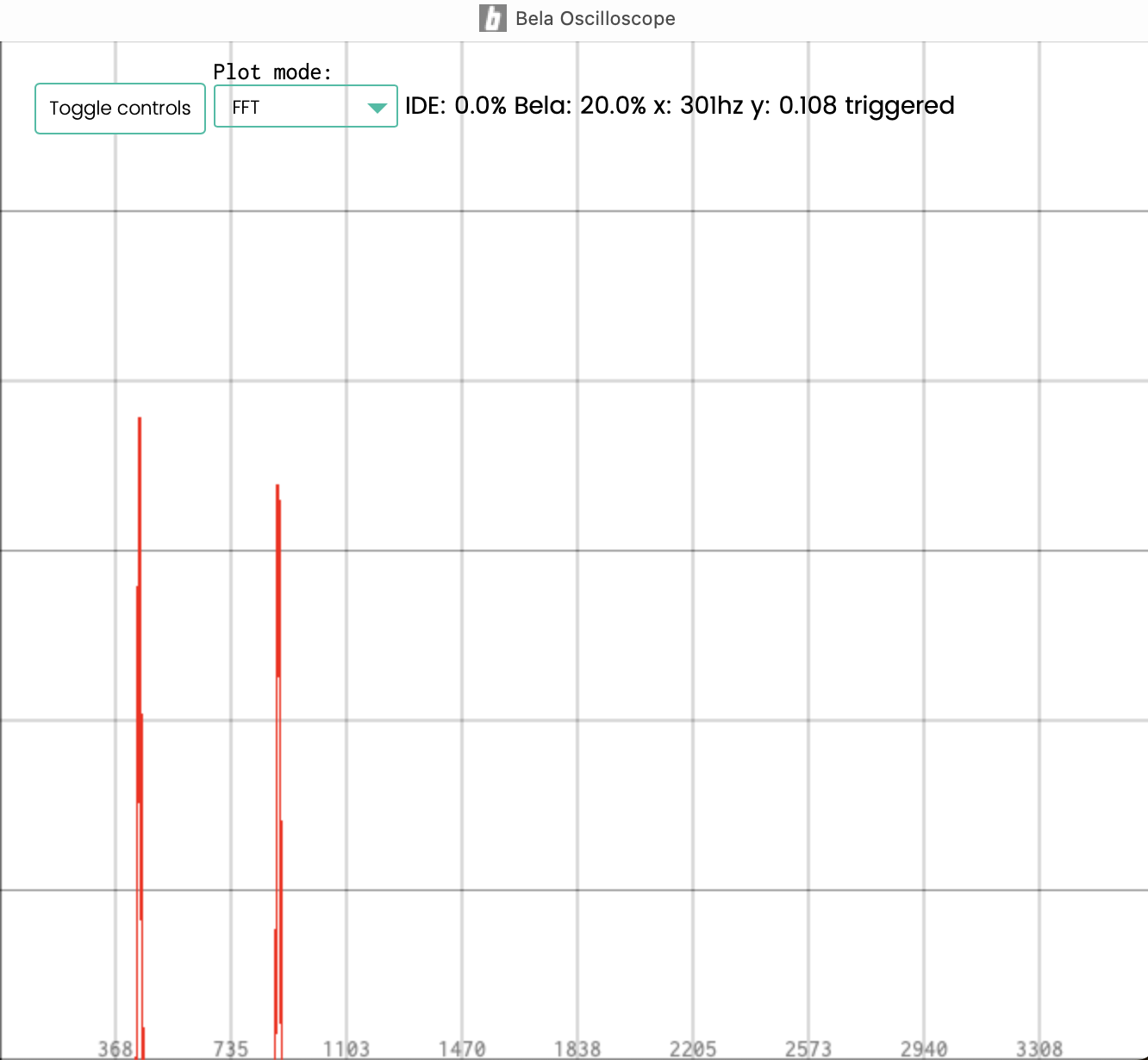
Das Signal ist als fft im folgenden Bild dargestellt. Die Basisfrequenz $f_{1}$ beträgt $440 Hz$. Die 2. Frequenz $f_{2}$ beträgt das doppelte, nämlich $2*f0 = 880 Hz$.